What is Zero Knowledge Proof (Developer POV)?#
Zero Knowledge proofs (or ZKP) allow developers to create mathematical proofs that a computation has been executed correctly, while not having to reveal all the data of this computation.
What are the applications of ZKP?#
There are three main areas of application:
Privacy: because not all data has to be revealed we can proof computations and facts while preserving privacy or secrecy of some part of the data.
Scalability and verified computation: usually to check that a computation has been executed correctly you would need to execute it and check the results are the same. With ZKP you can validate the mathematical proof of the computation, and in some systems this could require less time and space resources than executing the computation itself.
Interoperability and trustlessness: because ZKPs are based on mathematical proofs, an organisation or individual can trust a ZK proof without trusting other participants.
What are ZKP proving systems?#
Proving systems allow to create ZKP for arbitrary computations. They are like a computer system that can execute an arbitrary computation. A ZKP circuit is a definition for a proving system that proofs a specific computation. For example, for bubble sort algorithm you could write a circuit for a specific proving system that proofs bubble sort executions.
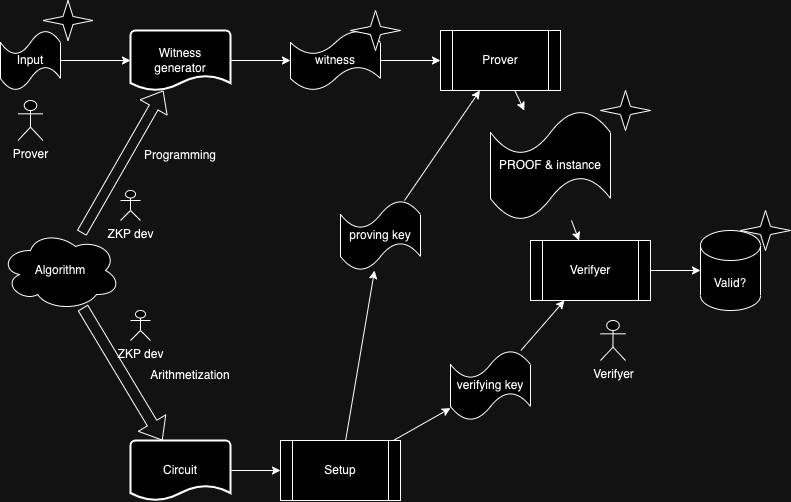
What are the elements of a ZKP circuit?#
The main elements are:
The witness: which is the data of the computation. The witness is made of many elements, sometimes called signals or cells. Some signals are public and other private, the public part is sometimes called the instance and the private part is sometimes called the advice. The witness usually contains the input and output of the computation, but also most or all its intermediate values (the trace).
Setup: it is a series of constraints or assertions over the witness data, that define which computations are valid.
Witness generation: an algorithm that helps calculating the right values for all the signals.
Proving and validation key: given a setup the proving system can generate a proving and validation pair of keys. Both can be made public.
Proof and prover: given a setup and a witness, the prover using the proving key can generate a proof. This proof will be valid if and only if the witness follows the setup constraints.
Validator: given a proof, the public part of the witness and a validation key, the validator can check the proof is valid using the proving system. Which means, to generate that proof the prover had to have a witness (in which this public part is part of) that followed the setup.
It is important to note that, if the prover and validator have agreed on the setup, they will have the same proving and validation keys, and they will not need to trust on each other.
What is a ZKP arithmetization?#
An arithmetization is the way to represent the setup to the proving system. It is very low level and based on polynomials. As a simile, if the proving system is a CPU, the arithmetization is its machine code.
What is a ZKP low-level DSL?#
It is a tool to write arithmetization in a more developer friendly way, but still very close to the arithmetization. If arithmetization is machine code, a ZKP low-level DSL is like assembly.
What is a ZKP high-level structured language?#
It allows to write the setup in a way that is closer to the way a developer thinks about the computation, and it gets compiled to the arithmetization. Following the previous simile a ZKP high-level structured language is like Python.
Chiquito is an example of ZKP high-level structured language that is based on steps.
What is a Finite Prime Field?#
In ZKP the witness signals are not made of bytes, they are elements (or values) of a Finite Prime Field. We need to understand how FPFs work in order to write circuits.
As a developer you can see it as a unsigned integer type where the maximum value is a prime minus one (p - 1 instead of 2^n-1) and addition and multiplication overflows as expected, so a + b = a + b mod p and a * b = a * b mod p.
Negative values are obtained by the formula a + (-a) mod p = 0.
The prime p is usually a very big number when used in ZKP, but we can see an easy example with p = 7.
The possible values would be 0, 1, 2, 3, 4, 5 and 6. If we go over p it overflows around to 0. So for example 6 + 1 = 0 or 5 + 3 = 1.
Then for example -3 + 3 mod 7 = 0 which is satisfied by 4 + 3 mod 7 = 0 => -3 = 4.
This is a very short summary of what you need to know about FPFs.
